EffTox, Wages & Tait, and BOIN12 - Efficacy & Toxicity Designs

Source: vignettes/A310-EfficacyToxicity.Rmd

Introduction

Seamless phase I/II designs extend the typical phase I or maximum tolerated dose-seeking approach by incorporating efficacy outcomes into the dose selection decision. Researchers will be motivated to escalate dose whilst there is a lack of efficacy and de-escalate under the presence of excess toxicity.

One of the earliest designs in this space was EffTox by P. F. Thall and Cook (2004). Their design uses logit models for the probability of toxicity and efficacy at the research doses, and allows the two events to be correlated in a joint model. Wages and Tait (2015) introduced a multi-stage design that uses response-adaptive randomisation to explore the doses. Most recently, Lin et al. (2020) introduced a generalisation of the BOIN Bayesian interval design for efficacy and toxicity outcomes called BOIN12. These designs are implemented in escalation and demonstrated below.

First, we must learn how to specify efficacy and toxicity outcomes in escalation. We do that in the next section.

Outcome nomenclature

In a joint phase I/II trial, where we have coincident efficacy and toxicity outcomes, we present outcomes in the individual patients using the letters:

  • T to show that toxicity without efficacy occurred in a patient;
  • E to show that efficacy without toxicity occurred in a patient;
  • N to show that neither occurred;
  • B to show that both occurred.

These outcome letters are strewn behind dose-levels to show the outcomes of patients in cohorts. To show that a cohort a three patients was given dose 2, with the first experiencing toxicity without efficacy, the second experiencing efficacy without toxicity, and the third experiencing both, we would use the outcome string:

outcomes <- '2TEB'

There are many more examples below.

EffTox

Thall & Cook (P. F. Thall and Cook 2004) introduced the EffTox design for dose-finding clinical trials where both efficacy and toxicity events guide dose selection decisions. We provide a brief recap of EffTox here, but full details are given in (P. F. Thall and Cook 2004; P. Thall, Cook, and Estey 2006; P. Thall et al. 2014).

For doses 𝐲=(y1,...,yn)\boldsymbol{y} = (y_1, ..., y_n), the authors define codified doses (x1,...,xn)(x_1, ..., x_n) using the transform

xi=logyi−∑j=1nlogyjnx_i = \log{y_i} - \sum_{j=1}^n \frac{\log{y_j}}{n}

The codified doses are used as the explanatory variables in logit models for the marginal probabilities of toxicity and efficacy:

logit πT=α+βx\text{logit } \pi_T = \alpha + \beta x

logit πE=γ+ζx+ηx2\text{logit } \pi_E = \gamma + \zeta x + \eta x^2

Let (Yj,Zj)(Y_j, Z_j) be random variables each taking values {0,1}\{0, 1\} representing the presence of efficacy and toxicity in patient jj.

Then the efficacy and toxicity events are associated by the joint probability function

Pr(Y=a,Z=b)=πa,b(πE,πT)=(πE)a(1−πE)1−a(πT)b(1−πT)1−b+(−1)a+b(πE)(1−πE)(πT)(1−πT)eψ−1eψ+1Pr(Y = a, Z = b) = \pi_{a,b}(\pi_E, \pi_T) = (\pi_E)^a (1-\pi_E)^{1-a} (\pi_T)^b (1-\pi_T)^{1-b} + (-1)^{a+b} (\pi_E) (1-\pi_E) (\pi_T) (1-\pi_T) \frac{e^\psi-1}{e^\psi+1}.

Normal priors are specified for the elements of the parameter vector 𝛉=(α,β,γ,ζ,η,ψ)\boldsymbol{\theta} = (\alpha, \beta, \gamma, \zeta, \eta, \psi).

At each dose update decision, the dose xx is acceptable if

Pr{πT(x,𝛉)<π¯T|data}>pT\text{Pr}\left\{ \pi_T(x, \boldsymbol{\theta}) < \overline{\pi}_T | \text{data} \right\} > p_T

and

Pr{πE(x,𝛉)>π_E|data}>pE\text{Pr}\left\{ \pi_E(x, \boldsymbol{\theta}) > \underline{\pi}_E | \text{data} \right\} > p_E

and is no more than than one position below the lowest dose-level given and no more than one position above the highest dose-level given. The net effect of these last two criteria is that untried doses may not be skipped in escalation or de-escalation. π_E,pE,π¯T,pT\underline{\pi}_E, p_E, \overline{\pi}_T, p_T are provided by the user as the trial scenario dictates.

The utility of dose xx, with efficacy πE(x,𝛉)\pi_E(x, \boldsymbol{\theta}) and toxicity πT(x,𝛉)\pi_T(x, \boldsymbol{\theta}) is

u(πE,πT)=1−((1−πE1−π1,E*)p+(πTπ2,T*)p)1pu(\pi_E, \pi_T) = 1 - \left( \left(\frac{1-\pi_E}{1-\pi_{1,E}^*}\right)^p + \left(\frac{\pi_T}{\pi_{2,T}^*}\right)^p \right) ^ \frac{1}{p}

where pp is calculated to intersect the points (π1,E*,0)(\pi_{1,E}^*, 0), (1,π2,T*)(1, \pi_{2,T}^*) and (π3,E*,π3,T*)(\pi_{3,E}^*, \pi_{3,T}^*) in the efficacy-toxicity plain. We refer to these as hinge points but that is not common nomenclature.

At the dose selection decision, the dose-level from the acceptable set with maximal utility is selected to be given to the next patient or cohort. If there are no acceptable doses, the trial stops and no dose is recommended.

There are several published EffTox examples, including explanations and tips on parameter choices (P. F. Thall and Cook 2004; P. Thall, Cook, and Estey 2006; P. Thall et al. 2014).

Wages & Tait

The design of Wages and Tait (2015) uses latent CRM models to estimate the probabilities of toxicity and efficacy, and two stages to identify the recommended dose. In the first stage, the design sequentially seeks the dose with probability of toxicity nearest to an upper toxicity threshold, like the classic CRM approach. In the second stage, the design adaptively randomises to the permissible doses, i.e. those with probability of toxicity not considered statistically too toxic, with greater randomisation weight given to those doses with higher estimated efficacy rates. The design uses a toxicity skeleton, like CRM, and several competing efficacy skeletons to accommodate that efficacy may not be monotonically increasing in dose.

BOIN12

The Bayesian Optimal Interval (BOIN) design was introduced by Liu and Yuan (2015). It is one of a series of dose-finding trial designs that works by partitioning the probability of toxicity into a set of intervals. These designs make dose-selection decisions that are determined by the interval in which the probability of toxicity for the current dose is believed to reside. The BOIN12 generalisation applies similar logic to co-primary binary toxicity and efficacy outcomes.

Implementation in escalation

To demonstrate the methods, let us consider the recommended dose after observing outcomes 1NNN 2EBT seeking a dose no more toxic than 0.3 with an associated efficacy probability of at least 0.5.

In each design, there will be many parameters that need to be set because these designs are comparatively complex. Ordinarily, parameter choices would be justified in light of the prevailing clinical scenario, and evaluated by simulation. For the purposes of illustration in this document, however, we are going to proceed with typical or general values.

library(escalation)

outcomes <- "1NNN 2EBT"

EffTox

For simplicity, we will use the parametersiation specified in an example investigating five doses in P. Thall et al. (2014):

p <- trialr::efftox_priors(
  alpha_mean = -7.9593, alpha_sd = 3.5487,
  beta_mean = 1.5482, beta_sd = 3.5018,
  gamma_mean = 0.7367, gamma_sd = 2.5423,
  zeta_mean = 3.4181, zeta_sd = 2.4406,
  eta_mean = 0, eta_sd = 0.2,
  psi_mean = 0, psi_sd = 1
)
real_doses = c(1.0, 2.0, 4.0, 6.6, 10.0)
num_doses <- length(real_doses)

et_model <- get_trialr_efftox(
  real_doses = real_doses,
  efficacy_hurdle = 0.5, toxicity_hurdle = 0.3,
  p_e = 0.1, p_t = 0.1,
  eff0 = 0.5, tox1 = 0.65,
  eff_star = 0.7, tox_star = 0.25,
  priors = p, 
  # Low MCMC sample size purely for speed in vignette:
  iter = 1000, chains = 1, seed = 2020
)
et_fit <- et_model %>% fit(outcomes)
et_fit
#> Patient-level data:
#> # A tibble: 6 × 5
#>   Patient Cohort  Dose   Tox   Eff
#>     <int>  <int> <int> <int> <int>
#> 1       1      1     1     0     0
#> 2       2      1     1     0     0
#> 3       3      1     1     0     0
#> 4       4      2     2     0     1
#> 5       5      2     2     1     1
#> 6       6      2     2     1     0
#> 
#> Dose-level data:
#> Warning: `...` must be empty in `format.tbl()`
#> Caused by error in `format_tbl()`:
#> ! `...` must be empty.
#> ✖ Problematic argument:
#> • digits = 3
#> # A tibble: 6 × 12
#>   dose     tox   eff     n empiric_tox_rate mean_prob_tox median_prob_tox
#>   <ord>  <dbl> <dbl> <dbl>            <dbl>         <dbl>           <dbl>
#> 1 NoDose     0     0     0            0             0               0    
#> 2 1          0     0     3            0             0.164           0.111
#> 3 2          2     2     3            0.667         0.298           0.265
#> 4 3          0     0     0          NaN             0.507           0.520
#> 5 4          0     0     0          NaN             0.600           0.691
#> 6 5          0     0     0          NaN             0.649           0.823
#> # ℹ 5 more variables: empiric_eff_rate <dbl>, mean_prob_eff <dbl>,
#> #   median_prob_eff <dbl>, admissible <lgl>, recommended <lgl>
#> 
#> The model uses a toxicity limit of 0.3.
#> The model uses an efficacy limit of 0.5.
#> The model advocates continuing at dose 3.
recommended_dose(et_fit)
#> [1] 3
continue(et_fit)
#> [1] TRUE
dose_admissible(et_fit)
#> [1] FALSE  TRUE  TRUE FALSE FALSE

Wages & Tait

For simplicity we will use the parametersiation specified in Wages and Tait (2015), tweaked slightly to reflect the dose-levels and targets specified in the EffTox example above.

tox_skeleton = c(0.08, 0.15, 0.22, 0.29, 0.36)

eff_skeletons = matrix(nrow = 9, ncol = num_doses)
eff_skeletons[1,] <- c(0.60, 0.50, 0.40, 0.30, 0.20)
eff_skeletons[2,] <- c(0.50, 0.60, 0.50, 0.40, 0.30)
eff_skeletons[3,] <- c(0.40, 0.50, 0.60, 0.50, 0.40)
eff_skeletons[4,] <- c(0.30, 0.40, 0.50, 0.60, 0.50)
eff_skeletons[5,] <- c(0.20, 0.30, 0.40, 0.50, 0.60)
eff_skeletons[6,] <- c(0.30, 0.40, 0.50, 0.60, 0.60)
eff_skeletons[7,] <- c(0.40, 0.50, 0.60, 0.60, 0.60)
eff_skeletons[8,] <- c(0.50, 0.60, 0.60, 0.60, 0.60)
eff_skeletons[9,] <- c(0.60, 0.60, 0.60, 0.60, 0.60)
eff_skeleton_weights = rep(1, nrow(eff_skeletons))

wt_model <- get_wages_and_tait(
  tox_skeleton = tox_skeleton,
  eff_skeletons = eff_skeletons,
  tox_limit = 0.3, eff_limit = 0.5,
  num_randomise = 20
)

The toxicity skeleton specified above plays exactly the equivalent role as seen in the CRM design. There are several efficacy skeletons to allow that efficacy may not be monotonic in dose. We use efficacy skeletons to reflect that: i) each dose may be the maximum, with monotonic increase and subsequent decrease relative to that dose; and ii) that each dose may be a plateau point, with equal efficacy at higher doses. In general, this generates 2n−12n - 1 efficacy skeletons in a trial of nn doses. The probabilities in the efficacy skeletons are less important than the shape the skeleton conveys because the average height of the dose-efficacy curve will be adjusted in Bayesian updating.

We fit the model to the outcomes:

wt_fit <- wt_model %>% fit(outcomes)

and see that a dose is advised for the next cohort:

recommended_dose(wt_fit)
#> [1] 1
continue(wt_fit)
#> [1] TRUE

Note that this design differs from EffTox in which doses it infers to be admissible. Different designs behave in different ways!

dose_admissible(wt_fit)
#> [1]  TRUE FALSE FALSE FALSE FALSE

Uncommonly seen in dose-finding designs, this design is a randomising design:

is_randomising(wt_fit)
#> [1] TRUE

Doses are assigned to patients in the first trial stage in a non-randomising way (i.e. the same outcomes fit to the same design will yield the same recommended dose). In contrast, doses are randomised in the second trial stage correlated to the modelled efficacy probability at each dose.

BOIN12

For illustration, we use the parameterisation presented and justified in Liu and Yuan (2015).

b_model <- get_boin12(
  num_doses = 5, phi_t = 0.3, phi_e = 0.5, u2 = 40, u3 = 60, n_star = 6
)

We fit the model to outcomes using the usual method:

b_fit <- b_model %>% fit(outcomes)

And we can obtain the usual information as presented in many places in these vignettes:

recommended_dose(b_fit)
#> [1] 1
continue(b_fit)
#> [1] TRUE
dose_admissible(b_fit)
#> [1] FALSE  TRUE  TRUE FALSE FALSE

Unlike EffTox and Wages & Tait, the BOIN12 design performs an additional step at the final dose recommendation to select the dose that is finally recommended. This same approach is used in BOIN and mTIP2, for instance. Read on.

Final dose selection

BOIN12, like some other designs, selects the final dose differently to how it selects doses mid-trial. To achieve this in escalation, we need an extra selector that will kick-in when the parent selector(s) have selected a non-NA dose but expressed continue == FALSE, i.e. signaled the trial ends now but we are interested in a dose. If used, it will almost surely come last in the selector chain:

b_model2 <- get_boin12(
  num_doses = 5, phi_t = 0.3, phi_e = 0.5, u2 = 40, u3 = 60, n_star = 6
) %>%
  stop_at_n(n = 12) %>%
  select_boin12_obd()

outcomes <- '1NNN 2NTN 2NNN 3BEN'
b_model2 %>% fit(outcomes) %>% recommended_dose()
#> [1] 3

Note we have forced the maximum sample size to 12 and provided outcomes for 12 patients so that the logic of select_boin12_obd is invoked.

In the above example, stop_at_n stopped the trial because the threshold sample size was met, and the underlying algorithm identified that at least one dose was worthy of selection. At this juncture, select_boin12_obd took over and applied the method described by the authors. Whilst the underlying selector(s) were busy conducting the trial (continue == TRUE), select_boin12_obd kept silent.

RDS tabulation

For convenience, we have also implemented BOIN12’s RDS (rank-based desirability score) algorithm:

boin12_rds(
 sample_sizes = c(0, 3, 6, 9),
 phi_t = 0.35,
 phi_e = 0.25,
 u1 = 100,
 u2 = 40,
 u3 = 60,
 u4 = 0,
 c_t = 0.95,
 c_e = 0.9,
 prior_alpha = 1,
 prior_beta = 1
)
#> # A tibble: 166 × 6
#>    Patients Toxicity Efficacy Admissible RDS   RDS_x
#>       <dbl>    <int>    <int> <chr>      <chr> <dbl>
#>  1        0        0        0 Admissible 60       60
#>  2        3        0        0 Admissible 35       35
#>  3        3        0        1 Admissible 55       55
#>  4        3        0        2 Admissible 76       76
#>  5        3        0        3 Admissible 91       91
#>  6        3        1        0 Admissible 24       24
#>  7        3        1        1 Admissible 44       44
#>  8        3        1        2 Admissible 63       63
#>  9        3        1        3 Admissible 80       80
#> 10        3        2        0 Admissible 13       13
#> # ℹ 156 more rows

The return data-frame comprises:

  • Patients, the number of patients
  • Toxicity, the number of patients experiencing toxicity events
  • Efficacy, the number of patients experiencing efficacy events
  • Admissible, a character label denoting admissibility status
  • RDS, a character label denoting the score in text format
  • RDS_x, the RDS in numerical form (i.e. appropriate for sorting)

Dose paths

As with all designs in escalation, we can use dose-paths to exhaustively calculate model advice for all possible future cohorts. However, first, a note of warning.

In phase 1/2 trials, there are four outcomes each patient may experience (listed above), so there are 10 distinct combinations of outcomes that a cohort of two patients may yield (n.b. we are counting combinations rather than permutations), and 20 combinations that a cohort of three may yield. This means that the size of a dose-path tree grows very quickly, so we must be modest in our aspirations here lest we be overwhelmed with information!

For example, after observing 1NN in an initial cohort of two patients, we will reproduce the dose-advice for the next two cohorts of two patients (i.e. 100 paths). For comparison, we will specify that the next dose will be 2. This starts the designs from a common place. Naturally, this option can be omitted and the design would start from whatever dose it recommended after seeing outcomes 1NN.

To visualise paths for the EffTox design, we run:

cohort_sizes <- c(2, 2)
outcomes <- "1NN"

et_paths <- et_model %>% 
  get_dose_paths(
    cohort_sizes = cohort_sizes, 
    previous_outcomes = outcomes,
    next_dose = 2
  )
#> You have requested 100 paths. Be patient.
#> Warning: The largest R-hat is 1.07, indicating chains have not mixed.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#r-hat

graph_paths(et_paths)

Had there been no previous outcomes (i.e. at the start of a new trial), we could have omitted the previous_outcomes parameter.

We can visualise the equivalent using the Wages & Tait design:

wt_paths <- wt_model %>% 
  get_dose_paths(
    cohort_sizes = cohort_sizes, 
    previous_outcomes = outcomes,
    next_dose = 2
  )
#> You have requested 100 paths. Be patient.

graph_paths(wt_paths)

and the BOIN12 design:

b_paths <- b_model %>% 
  get_dose_paths(
    cohort_sizes = cohort_sizes, 
    previous_outcomes = outcomes,
    next_dose = 2
  )
#> You have requested 100 paths. Be patient.

graph_paths(b_paths)

As we might expect, we see distinct differences in the dose decisions by design. EffTox will escalate in this example much more readily.

For more information on working with dose-paths, refer to the dose-paths vignette.

Simulation

We can simulate trials using all designs in escalation. Computation using Bayesian designs can be computationally costly so for the purposes of illustration in this vignette, we will simulate just twenty trials per design at the following true toxicity and efficacy curves:

n_sim <- 20
true_prob_tox = c(0.02, 0.12, 0.17, 0.38, 0.55)
true_prob_eff = c(0.25, 0.27, 0.52, 0.54, 0.54)

To promote comparability, we will give each design just 12 patients (again, just for illustration) and prevent each design from skipping doses in escalation.

To simulate under the EffTox design, we run:

et_model <- get_trialr_efftox(
  real_doses = real_doses,
  efficacy_hurdle = 0.5, toxicity_hurdle = 0.3,
  p_e = 0.1, p_t = 0.1,
  eff0 = 0.5, tox1 = 0.65,
  eff_star = 0.7, tox_star = 0.25,
  priors = p, 
  # Low MCMC sample size purely for speed in vignette:
  iter = 2000, chains = 1, 
) %>% 
  dont_skip_doses() %>% 
  stop_at_n(n = 12)

set.seed(2025)
et_sims <- et_model %>% 
  simulate_trials(
    num_sims = n_sim, 
    true_prob_tox = true_prob_tox,
    true_prob_eff = true_prob_tox
  )
et_sims
#> Number of iterations: 20 
#> 
#> Number of doses: 5 
#> 
#> True probability of toxicity:
#>    1    2    3    4    5 
#> 0.02 0.12 0.17 0.38 0.55 
#> 
#> True probability of efficacy:
#>    1    2    3    4    5 
#> 0.02 0.12 0.17 0.38 0.55 
#> 
#> Probability of recommendation:
#> NoDose      1      2      3      4      5 
#>   0.10   0.00   0.00   0.05   0.35   0.50 
#> 
#> Probability of administration:
#>     1     2     3     4     5 
#> 0.253 0.253 0.304 0.190 0.000 
#> 
#> Sample size:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    9.00   12.00   12.00   11.85   12.00   12.00 
#> 
#> Total toxicities:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    0.00    1.00    2.00    2.05    3.00    5.00 
#> 
#> Total efficacies:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    0.00    1.00    2.00    1.75    3.00    4.00 
#> 
#> Trial duration:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>   5.844   8.951   9.953  10.759  12.937  22.432

And under the Wages & Tait design:

wt_model <- get_wages_and_tait(
  tox_skeleton = tox_skeleton,
  eff_skeletons = eff_skeletons,
  tox_limit = 0.3, eff_limit = 0.5,
  num_randomise = 20
) %>% 
  dont_skip_doses() %>% 
  stop_at_n(n = 12)

set.seed(2025)
wt_sims <- wt_model %>% 
  simulate_trials(
    num_sims = n_sim, 
    true_prob_tox = true_prob_tox,
    true_prob_eff = true_prob_tox
  )
wt_sims
#> Number of iterations: 20 
#> 
#> Number of doses: 5 
#> 
#> True probability of toxicity:
#>    1    2    3    4    5 
#> 0.02 0.12 0.17 0.38 0.55 
#> 
#> True probability of efficacy:
#>    1    2    3    4    5 
#> 0.02 0.12 0.17 0.38 0.55 
#> 
#> Probability of recommendation:
#> NoDose      1      2      3      4      5 
#>   0.15   0.10   0.35   0.25   0.10   0.05 
#> 
#> Probability of administration:
#>      1      2      3      4      5 
#> 0.1972 0.3239 0.2958 0.1549 0.0282 
#> 
#> Sample size:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    3.00   12.00   12.00   10.65   12.00   12.00 
#> 
#> Total toxicities:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    0.00    1.00    2.00    1.75    2.25    5.00 
#> 
#> Total efficacies:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    0.00    1.00    1.50    1.65    2.00    5.00 
#> 
#> Trial duration:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  0.3197  6.5617 11.1565 11.0194 13.9553 19.9895

And under the BOIN12 design:

b_model <- get_boin12(
  num_doses = 5, phi_t = 0.3, phi_e = 0.5, u2 = 40, u3 = 60, n_star = 6
) %>%
  dont_skip_doses() %>% 
  stop_at_n(n = 12) %>% 
  select_boin12_obd()
  
set.seed(2025)
b_sims <- b_model %>% 
  simulate_trials(
    num_sims = n_sim, 
    true_prob_tox = true_prob_tox,
    true_prob_eff = true_prob_tox
  )
b_sims
#> Number of iterations: 20 
#> 
#> Number of doses: 5 
#> 
#> True probability of toxicity:
#>    1    2    3    4    5 
#> 0.02 0.12 0.17 0.38 0.55 
#> 
#> True probability of efficacy:
#>    1    2    3    4    5 
#> 0.02 0.12 0.17 0.38 0.55 
#> 
#> Probability of recommendation:
#> NoDose      1      2      3      4      5 
#>   0.00   0.20   0.10   0.35   0.35   0.00 
#> 
#> Probability of administration:
#>     1     2     3     4     5 
#> 0.250 0.263 0.263 0.225 0.000 
#> 
#> Sample size:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>      12      12      12      12      12      12 
#> 
#> Total toxicities:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    1.00    1.00    2.00    1.95    2.25    4.00 
#> 
#> Total efficacies:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>    0.00    1.00    2.00    2.15    3.00    5.00 
#> 
#> Trial duration:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>   6.619   9.554  10.885  11.179  12.384  16.512

To compare designs, however, it is much more efficient to use the method presented in Sweeting et al. (2024) using simulate_compare:

designs <- list(
  EffTox = et_model,
  WagesTait = wt_model,
  BOIN12 = b_model
)

sims <- simulate_compare(
  designs = designs, 
  num_sims = n_sim, 
  true_prob_tox = true_prob_tox,
  true_prob_eff = true_prob_tox
)
#> Running BOIN12 
#> Running EffTox 
#> Running WagesTait
convergence_plot(sims)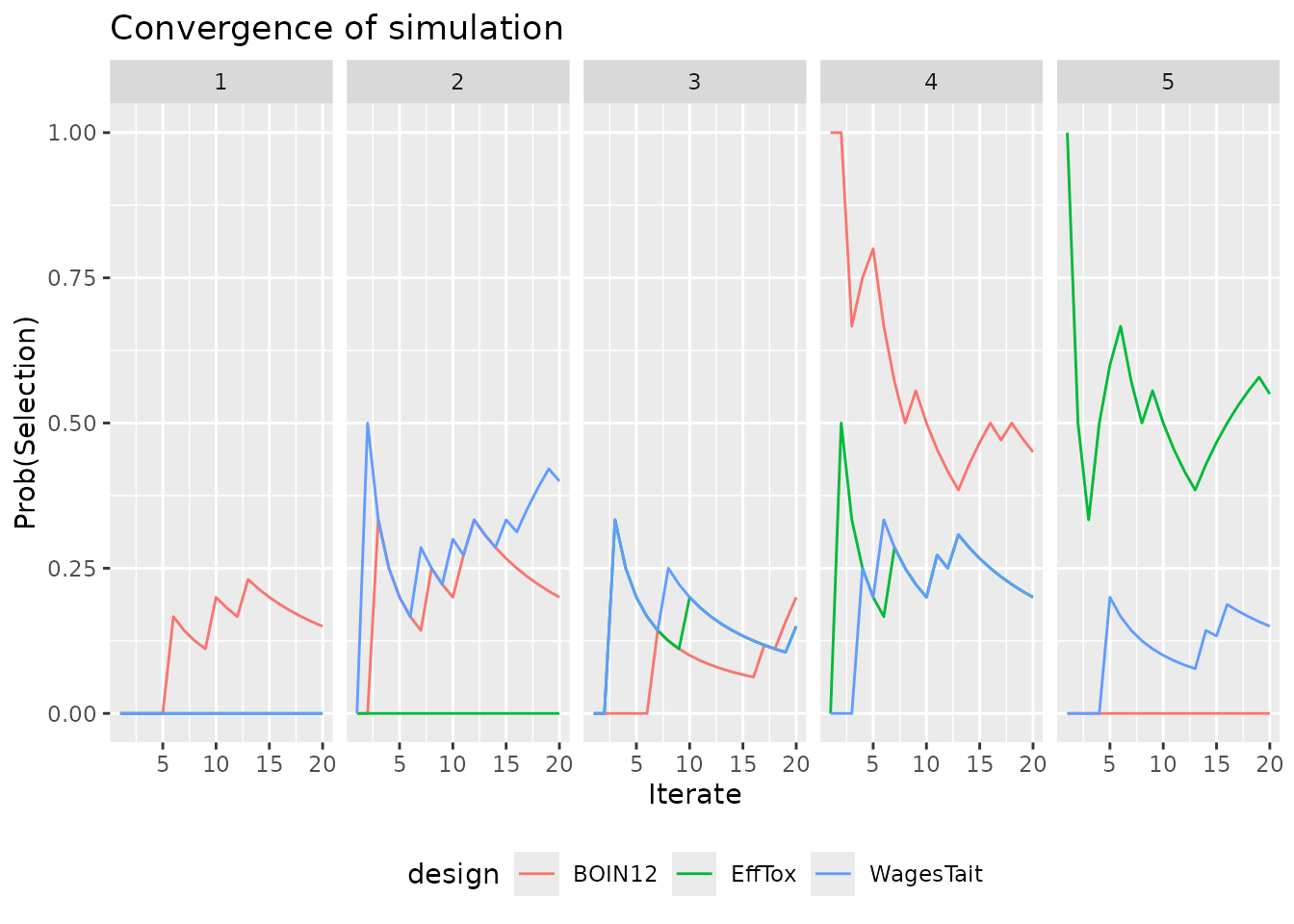

We stress again, the design parameters in these examples have been chosen in haste merely for illustration. The work presented here in no way constitutes a valid comparison of these three designs.

For more information on running dose-finding simulations, refer to the simulation vignette.

References

Lin, Ruitao, Yanhong Zhou, Fangrong Yan, Daniel Li, and Ying Yuan. 2020. “BOIN12: Bayesian Optimal Interval Phase i/II Trial Design for Utility-Based Dose Finding in Immunotherapy and Targeted Therapies.” JCO Precision Oncology 4: 1393–1402.
Liu, Suyu, and Ying Yuan. 2015. “Bayesian Optimal Interval Designs for Phase I Clinical Trials.” Journal of the Royal Statistical Society: Series C (Applied Statistics) 64 (3): 507–23. https://doi.org/10.1111/rssc.12089.
Sweeting, Michael, Daniel Slade, Daniel Jackson, and Kristian Brock. 2024. “Potential Outcome Simulation for Efficient Head-to-Head Comparison of Adaptive Dose-Finding Designs.” arXiv Preprint arXiv:2402.15460.
Thall, Peter F, and John D Cook. 2004. “Dose-Finding Based on Efficacy–Toxicity Trade-Offs.” Biometrics 60 (3): 684–93.
Thall, PF, JD Cook, and EH Estey. 2006. “Adaptive Dose Selection Using Efficacy-Toxicity Trade-Offs: Illustrations and Practical Considerations.” Journal of Biopharmaceutical Statistics 16 (5): 623–38. https://doi.org/10.1080/10543400600860394.
Thall, PF, RC Herrick, HQ Nguyen, JJ Venier, and JC Norris. 2014. “Effective Sample Size for Computing Prior Hyperparameters in Bayesian Phase I-II Dose-Finding.” Clinical Trials 11 (6): 657–66. https://doi.org/10.1177/1740774514547397.
Wages, Nolan A, and Christopher Tait. 2015. “Seamless Phase i/II Adaptive Design for Oncology Trials of Molecularly Targeted Agents.” Journal of Biopharmaceutical Statistics 25 (5): 903–20.